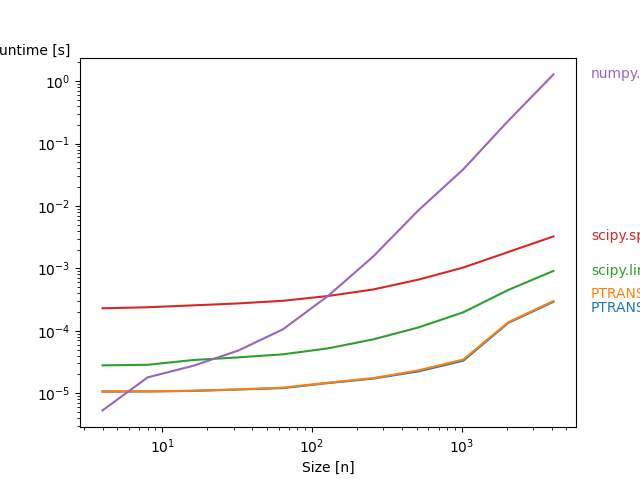
4. Example: Performance for full matrices

Here we compare all algorithms for solving pentadiagonal systems provided by pentapy (except umf) using a full quadratic matrix as input.

To use this script you need to have the following packages installed:

• scipy

• perfplot

• matplotlib

Overall ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 100% 0:00:00
Kernels ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 100% 0:00:00

import numpy as np
import perfplot

from pentapy import solve, tools


def get_les(size):
    mat = (np.random.random((5, size)) - 0.5) * 1e-5
    V = np.array(np.random.random(size) * 1e5)
    M = tools.create_full(mat)
    return M, V


def solve_1(in_val):
    """PTRANS-I"""
    mat, V = in_val
    return solve(mat, V, is_flat=False, solver=1)


def solve_2(in_val):
    """PTRANS-II"""
    mat, V = in_val
    return solve(mat, V, is_flat=False, solver=2)


def solve_3(in_val):
    mat, V = in_val
    return solve(mat, V, is_flat=False, solver=3)


def solve_4(in_val):
    mat, V = in_val
    return solve(mat, V, is_flat=False, solver=4)


def solve_5(in_val):
    mat, V = in_val
    return np.linalg.solve(mat, V)


perfplot.show(
    setup=get_les,
    kernels=[solve_1, solve_2, solve_3, solve_4, solve_5],
    labels=[
        "PTRANS-I",
        "PTRANS-II",
        "scipy.linalg.solve_banded",
        "scipy.sparse.linalg.spsolve",
        "numpy.linalg.solve",
    ],
    n_range=[2**k for k in range(2, 13)],
    xlabel="Size [n]",
    logy=True,
)