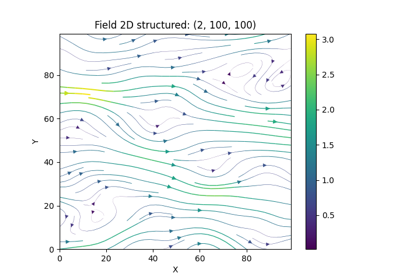
Random Vector Field Generation¶
In 1970, Kraichnan was the first to suggest a randomization method. For studying the diffusion of single particles in a random incompressible velocity field, he came up with a randomization method which includes a projector which ensures the incompressibility of the vector field.
Without loss of generality we assume that the mean velocity 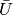 is oriented
towards the direction of the first basis vector
is oriented
towards the direction of the first basis vector 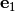 . Our goal is now to
generate random fluctuations with a given covariance model around this mean velocity.
And at the same time, making sure that the velocity field remains incompressible or
in other words, ensure
. Our goal is now to
generate random fluctuations with a given covariance model around this mean velocity.
And at the same time, making sure that the velocity field remains incompressible or
in other words, ensure 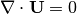 .
This can be done by using the randomization method we already know, but adding a
projector to every mode being summed:
.
This can be done by using the randomization method we already know, but adding a
projector to every mode being summed:
![\mathbf{U}(\mathbf{x}) = \bar{U} \mathbf{e}_1 - \sqrt{\frac{\sigma^{2}}{N}}
\sum_{i=1}^{N} \mathbf{p}(\mathbf{k}_i) \left[ Z_{1,i}
\cos\left( \langle \mathbf{k}_{i}, \mathbf{x} \rangle \right)
+ \sin\left( \langle \mathbf{k}_{i}, \mathbf{x} \rangle \right) \right]](../../_images/math/53a0aaf1241e8104a8d0f1cb038c4e44a0f147f9.png)
with the projector
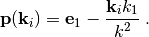
By calculating 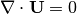 , it can be verified, that
the resulting field is indeed incompressible.
, it can be verified, that
the resulting field is indeed incompressible.