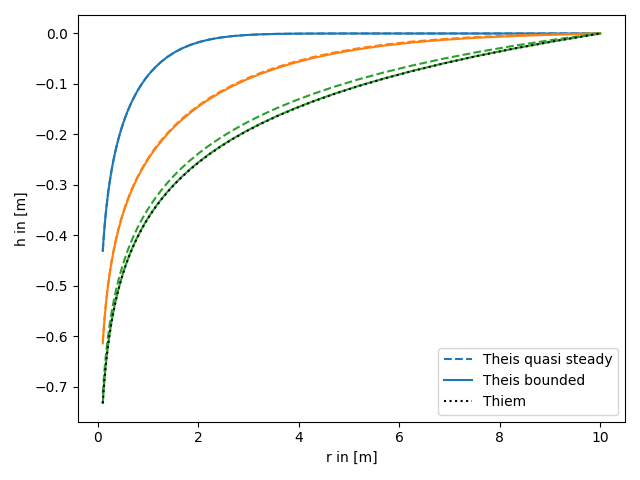
Quasi steady convergence

The quasi steady is reached, when the radial shape of the drawdown in not changing anymore.

import numpy as np
from matplotlib import pyplot as plt

from anaflow import theis, thiem

time = [10, 100, 1000]
rad = np.geomspace(0.1, 10)
r_ref = 10.0

head_ref = theis(
    time,
    np.full_like(rad, r_ref),
    storage=1e-3,
    transmissivity=1e-4,
    rate=-1e-4,
)
head1 = (
    theis(time, rad, storage=1e-3, transmissivity=1e-4, rate=-1e-4) - head_ref
)
head2 = theis(
    time, rad, storage=1e-3, transmissivity=1e-4, rate=-1e-4, r_bound=r_ref
)
head3 = thiem(rad, r_ref, transmissivity=1e-4, rate=-1e-4)

for i, step in enumerate(time):
    label_1 = "Theis quasi steady" if i == 0 else None
    label_2 = "Theis bounded" if i == 0 else None
    plt.plot(rad, head1[i], label=label_1, color="C" + str(i), linestyle="--")
    plt.plot(rad, head2[i], label=label_2, color="C" + str(i))

plt.plot(rad, head3, label="Thiem", color="k", linestyle=":")

plt.xlabel("r in [m]")
plt.ylabel("h in [m]")
plt.legend()
plt.tight_layout()
plt.show()