GSTools Quickstart

Get in Touch!
Youtube Tutorial on GSTools
Purpose
GeoStatTools provides geostatistical tools for various purposes:
random field generation
simple, ordinary, universal and external drift kriging
conditioned field generation
incompressible random vector field generation
(automated) variogram estimation and fitting
directional variogram estimation and modelling
data normalization and transformation
many readily provided and even user-defined covariance models
metric spatio-temporal modelling
plotting and exporting routines
Installation
conda
GSTools can be installed via conda on Linux, Mac, and Windows. Install the package by typing the following command in a command terminal:
conda install gstools
In case conda forge is not set up for your system yet, see the easy to follow instructions on conda forge. Using conda, the parallelized version of GSTools should be installed.
pip
GSTools can be installed via pip on Linux, Mac, and Windows. On Windows you can install WinPython to get Python and pip running. Install the package by typing the following into command in a command terminal:
pip install gstools
To get the latest development version you can install it directly from GitHub:
pip install git+git://github.com/GeoStat-Framework/GSTools.git@main
If something went wrong during installation, try the -I flag from pip.
Speeding up GSTools by parallelization
To enable the OpenMP support, you have to provide a C compiler and OpenMP.
Parallel support is controlled by an environment variable GSTOOLS_BUILD_PARALLEL,
that can be 0 or 1 (interpreted as 0 if not present).
GSTools then needs to be installed from source:
export GSTOOLS_BUILD_PARALLEL=1
pip install --no-binary=gstools gstools
Note, that the --no-binary=gstools option forces pip to not use a wheel for GSTools.
For the development version, you can do almost the same:
export GSTOOLS_BUILD_PARALLEL=1
pip install git+git://github.com/GeoStat-Framework/GSTools.git@main
Using experimental GSTools-Core for even more speed
You can install the optional dependency GSTools-Core,
which is a re-implementation of the main algorithms used in GSTools. The new
package uses the language Rust and it should be faster (in some cases by orders
of magnitude), safer, and it will potentially completely replace the current
standard implementation in Cython. Once the package GSTools-Core is available
on your machine, it will be used by default. In case you want to switch back to
the Cython implementation, you can set gstools.config.USE_RUST=False in
your code. This also works at runtime. You can install the optional dependency
e.g. by
pip install gstools[rust]
or by manually installing the package
pip install gstools-core
GSTools-Core will automatically use all your cores in parallel, without having
to use OpenMP or a local C compiler.
In case you want to restrict the number of threads used, you can set the
environment variable RAYON_NUM_THREADS to the desired amount.
Citation
If you are using GSTools in your publication please cite our paper:
Müller, S., Schüler, L., Zech, A., and Heße, F.: GSTools v1.3: a toolbox for geostatistical modelling in Python, Geosci. Model Dev., 15, 3161–3182, https://doi.org/10.5194/gmd-15-3161-2022, 2022.
You can cite the Zenodo code publication of GSTools by:
Sebastian Müller & Lennart Schüler. GeoStat-Framework/GSTools. Zenodo. https://doi.org/10.5281/zenodo.1313628
If you want to cite a specific version, have a look at the Zenodo site.
Tutorials and Examples
The documentation also includes some tutorials, showing the most important use cases of GSTools, which are
Spatial Random Field Generation
The core of this library is the generation of spatial random fields. These fields are generated using the randomisation method, described by Heße et al. 2014.
Examples
Gaussian Covariance Model
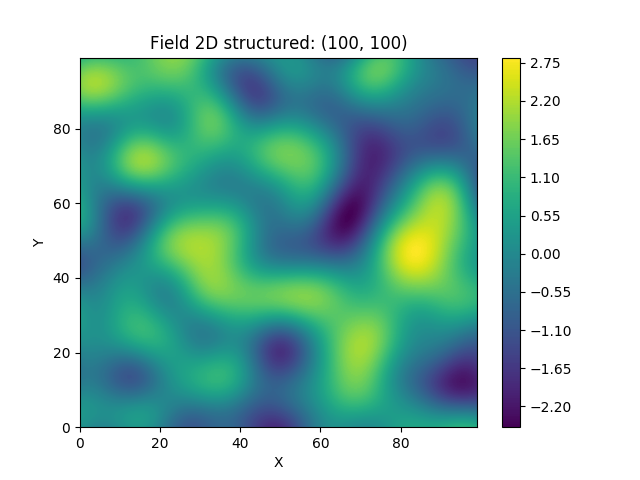
This is an example of how to generate a 2 dimensional spatial random field (SRF)
with a Gaussian covariance model.
import gstools as gs
# structured field with a size 100x100 and a grid-size of 1x1
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.plot()
GSTools also provides support for geographic coordinates. This works perfectly well with cartopy.
import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import gstools as gs
# define a structured field by latitude and longitude
lat = lon = range(-80, 81)
model = gs.Gaussian(latlon=True, len_scale=777, geo_scale=gs.KM_SCALE)
srf = gs.SRF(model, seed=12345)
field = srf.structured((lat, lon))
# Orthographic plotting with cartopy
ax = plt.subplot(projection=ccrs.Orthographic(-45, 45))
cont = ax.contourf(lon, lat, field, transform=ccrs.PlateCarree())
ax.coastlines()
ax.set_global()
plt.colorbar(cont)

A similar example but for a three dimensional field is exported to a VTK file, which can be visualized with ParaView or PyVista in Python:
import gstools as gs
# structured field with a size 100x100x100 and a grid-size of 1x1x1
x = y = z = range(100)
model = gs.Gaussian(dim=3, len_scale=[16, 8, 4], angles=(0.8, 0.4, 0.2))
srf = gs.SRF(model)
srf((x, y, z), mesh_type='structured')
srf.vtk_export('3d_field') # Save to a VTK file for ParaView
mesh = srf.to_pyvista() # Create a PyVista mesh for plotting in Python
mesh.contour(isosurfaces=8).plot()

Estimating and fitting variograms
The spatial structure of a field can be analyzed with the variogram, which contains the same information as the covariance function.
All covariance models can be used to fit given variogram data by a simple interface.
Examples
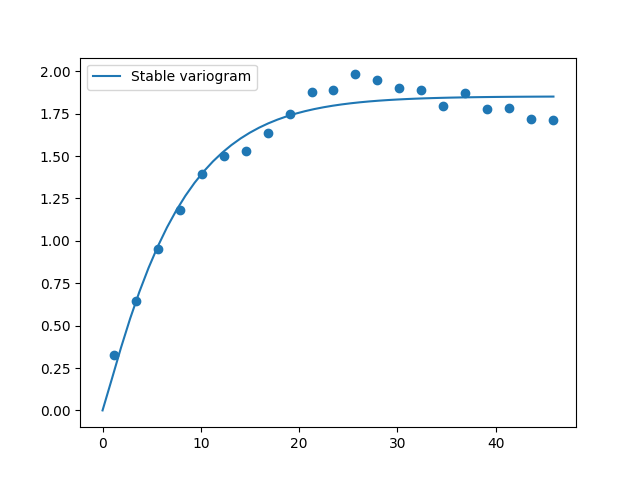
This is an example of how to estimate the variogram of a 2 dimensional unstructured field and estimate the parameters of the covariance model again.
import numpy as np
import gstools as gs
# generate a synthetic field with an exponential model
x = np.random.RandomState(19970221).rand(1000) * 100.
y = np.random.RandomState(20011012).rand(1000) * 100.
model = gs.Exponential(dim=2, var=2, len_scale=8)
srf = gs.SRF(model, mean=0, seed=19970221)
field = srf((x, y))
# estimate the variogram of the field
bin_center, gamma = gs.vario_estimate((x, y), field)
# fit the variogram with a stable model. (no nugget fitted)
fit_model = gs.Stable(dim=2)
fit_model.fit_variogram(bin_center, gamma, nugget=False)
# output
ax = fit_model.plot(x_max=max(bin_center))
ax.scatter(bin_center, gamma)
print(fit_model)
Which gives:
Stable(dim=2, var=1.85, len_scale=7.42, nugget=0.0, anis=[1.0], angles=[0.0], alpha=1.09)
Kriging and Conditioned Random Fields
An important part of geostatistics is Kriging and conditioning spatial random fields to measurements. With conditioned random fields, an ensemble of field realizations with their variability depending on the proximity of the measurements can be generated.
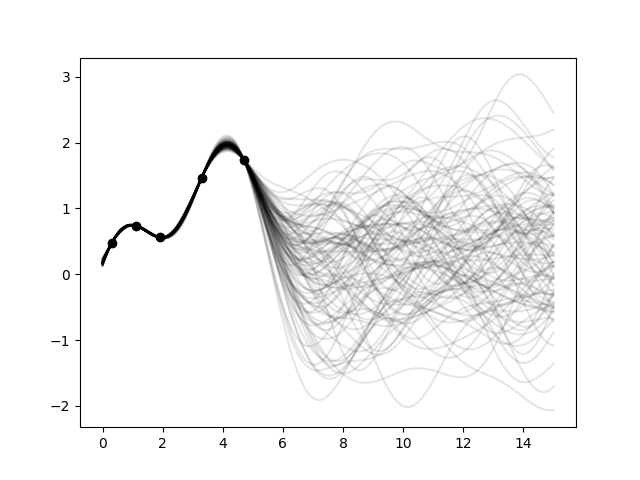
Example
For better visualization, we will condition a 1d field to a few “measurements”, generate 100 realizations and plot them:
import numpy as np
import matplotlib.pyplot as plt
import gstools as gs
# conditions
cond_pos = [0.3, 1.9, 1.1, 3.3, 4.7]
cond_val = [0.47, 0.56, 0.74, 1.47, 1.74]
# conditioned spatial random field class
model = gs.Gaussian(dim=1, var=0.5, len_scale=2)
krige = gs.krige.Ordinary(model, cond_pos, cond_val)
cond_srf = gs.CondSRF(krige)
# same output positions for all ensemble members
grid_pos = np.linspace(0.0, 15.0, 151)
cond_srf.set_pos(grid_pos)
# seeded ensemble generation
seed = gs.random.MasterRNG(20170519)
for i in range(100):
field = cond_srf(seed=seed(), store=f"field_{i}")
plt.plot(grid_pos, field, color="k", alpha=0.1)
plt.scatter(cond_pos, cond_val, color="k")
plt.show()
User defined covariance models
One of the core-features of GSTools is the powerful
CovModel
class, which allows to easy define covariance models by the user.
Example
Here we re-implement the Gaussian covariance model by defining just the
correlation function,
which takes a non-dimensional distance h = r/l
import numpy as np
import gstools as gs
# use CovModel as the base-class
class Gau(gs.CovModel):
def cor(self, h):
return np.exp(-h**2)
And that’s it! With Gau you now have a fully working covariance model,
which you could use for field generation or variogram fitting as shown above.
Incompressible Vector Field Generation
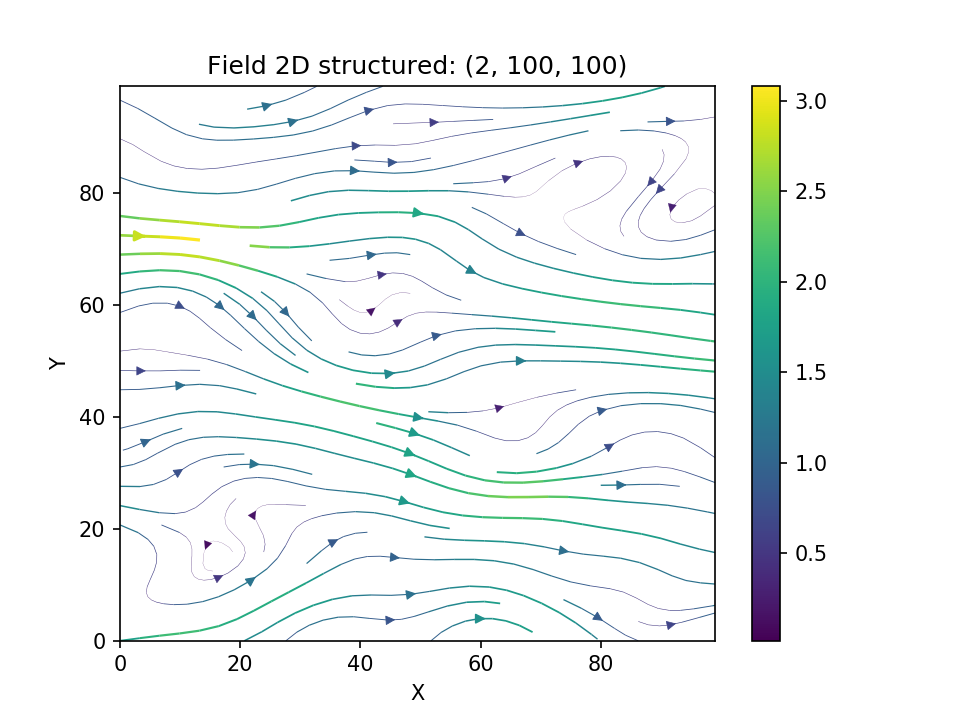
Using the original Kraichnan method, incompressible random spatial vector fields can be generated.
Example
import numpy as np
import gstools as gs
x = np.arange(100)
y = np.arange(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model, generator='VectorField', seed=19841203)
srf((x, y), mesh_type='structured')
srf.plot()
yielding
VTK/PyVista Export
After you have created a field, you may want to save it to file, so we provide
a handy VTK export routine using the vtk_export() or you could
create a VTK/PyVista dataset for use in Python with to to_pyvista() method:
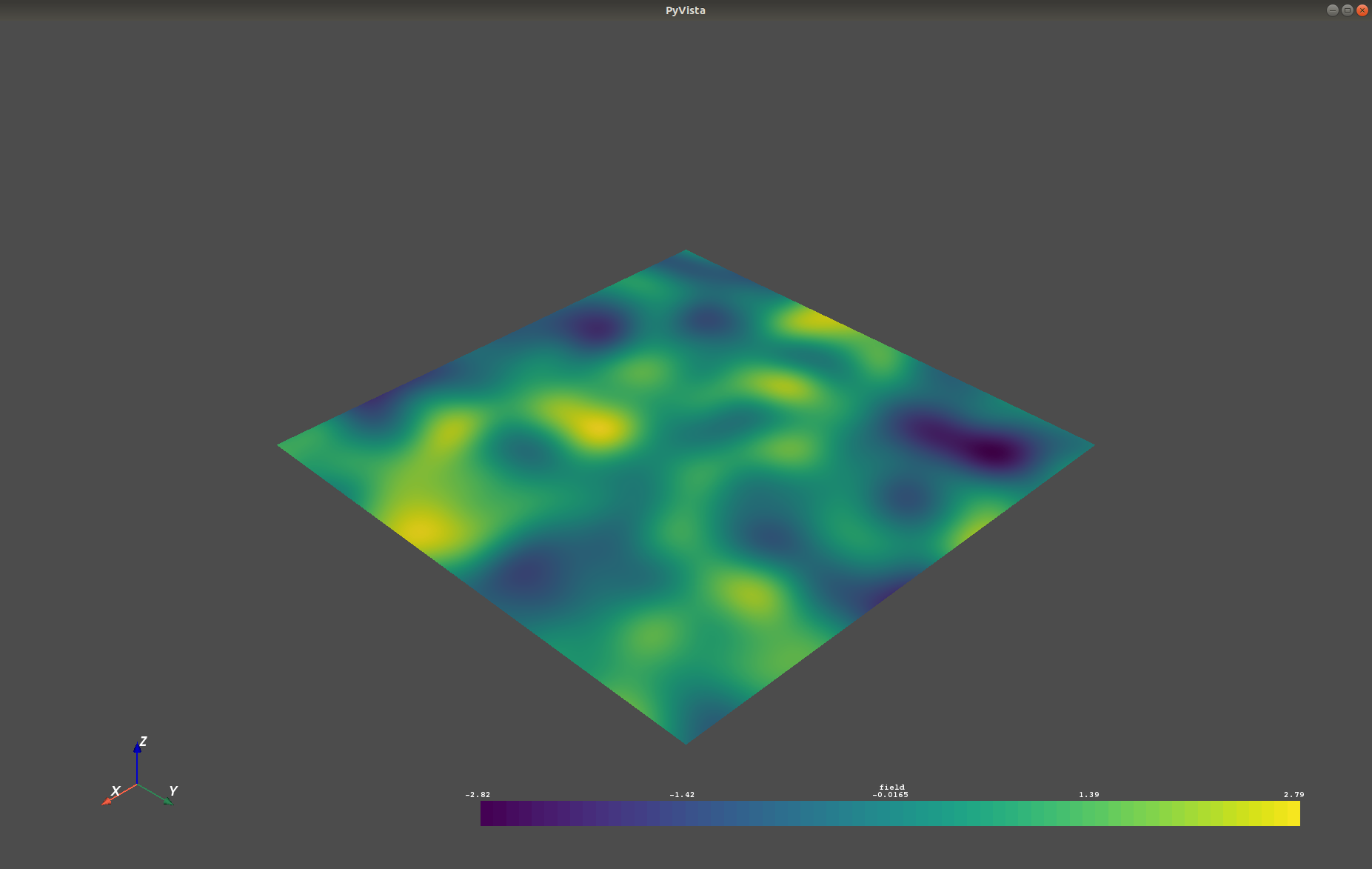
import gstools as gs
x = y = range(100)
model = gs.Gaussian(dim=2, var=1, len_scale=10)
srf = gs.SRF(model)
srf((x, y), mesh_type='structured')
srf.vtk_export("field") # Saves to a VTK file
mesh = srf.to_pyvista() # Create a VTK/PyVista dataset in memory
mesh.plot()
Which gives a RectilinearGrid VTK file field.vtr or creates a PyVista mesh
in memory for immediate 3D plotting in Python.
Requirements
Optional
Contact
You can contact us via info@geostat-framework.org.




