Truncated Power Law Variograms

GSTools also implements truncated power law variograms, which can be represented as a superposition of scale dependant modes in form of standard variograms, which are truncated by a lower- \(\ell_{\mathrm{low}}\) and an upper length-scale \(\ell_{\mathrm{up}}\).

This example shows the truncated power law (TPLStable) based on the Stable covariance model and is given by

\[\gamma_{\ell_{\mathrm{low}},\ell_{\mathrm{up}}}(r) = \intop_{\ell_{\mathrm{low}}}^{\ell_{\mathrm{up}}} \gamma(r,\lambda) \frac{\rm d \lambda}{\lambda}\]

with Stable modes on each scale:

\[\begin{split}\gamma(r,\lambda) &= \sigma^2(\lambda)\cdot\left(1- \exp\left[- \left(\frac{r}{\lambda}\right)^{\alpha}\right] \right)\\ \sigma^2(\lambda) &= C\cdot\lambda^{2H}\end{split}\]

which gives Gaussian modes for alpha=2 or Exponential modes for alpha=1.

For \(\ell_{\mathrm{low}}=0\) this results in:

\[\begin{split}\gamma_{\ell_{\mathrm{up}}}(r) &= \sigma^2_{\ell_{\mathrm{up}}}\cdot\left(1- \frac{2H}{\alpha} \cdot E_{1+\frac{2H}{\alpha}} \left[\left(\frac{r}{\ell_{\mathrm{up}}}\right)^{\alpha}\right] \right) \\ \sigma^2_{\ell_{\mathrm{up}}} &= C\cdot\frac{\ell_{\mathrm{up}}^{2H}}{2H}\end{split}\]

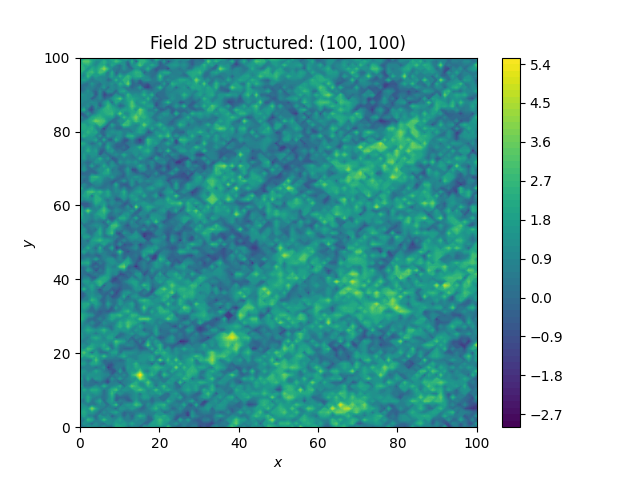
import numpy as np

import gstools as gs

x = y = np.linspace(0, 100, 100)
model = gs.TPLStable(
    dim=2,  # spatial dimension
    var=1,  # variance (C is calculated internally, so variance is actually 1)
    len_low=0,  # lower truncation of the power law
    len_scale=10,  # length scale (a.k.a. range), len_up = len_low + len_scale
    nugget=0.1,  # nugget
    anis=0.5,  # anisotropy between main direction and transversal ones
    angles=np.pi / 4,  # rotation angles
    alpha=1.5,  # shape parameter from the stable model
    hurst=0.7,  # hurst coefficient from the power law
)
srf = gs.SRF(model, mean=1.0, seed=19970221)
srf.structured([x, y])
srf.plot()