Note
Go to the end to download the full example code
Ordinary Kriging
Ordinary kriging will estimate an appropriate mean of the field, based on the given observations/conditions and the covariance model used.
The resulting system of equations for \(W\) is given by:
\[\begin{split}\begin{pmatrix}W\\\mu\end{pmatrix} = \begin{pmatrix}
c(x_1,x_1) & \cdots & c(x_1,x_n) &1 \\
\vdots & \ddots & \vdots & \vdots \\
c(x_n,x_1) & \cdots & c(x_n,x_n) & 1 \\
1 &\cdots& 1 & 0
\end{pmatrix}^{-1}
\begin{pmatrix}c(x_1,x_0) \\ \vdots \\ c(x_n,x_0) \\ 1\end{pmatrix}\end{split}\]
Thereby \(c(x_i,x_j)\) is the covariance of the given observations and \(\mu\) is a Lagrange multiplier to minimize the kriging error and estimate the mean.
Example
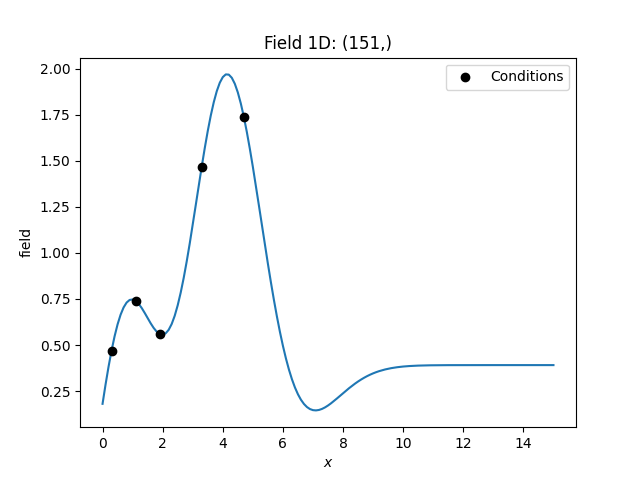
Here we use ordinary kriging in 1D (for plotting reasons) with 5 given observations/conditions.
The estimated mean can be accessed by krig.mean.
import numpy as np
from gstools import Gaussian, krige
# condtions
cond_pos = [0.3, 1.9, 1.1, 3.3, 4.7]
cond_val = [0.47, 0.56, 0.74, 1.47, 1.74]
# resulting grid
gridx = np.linspace(0.0, 15.0, 151)
# spatial random field class
model = Gaussian(dim=1, var=0.5, len_scale=2)
krig = krige.Ordinary(model, cond_pos=cond_pos, cond_val=cond_val)
krig(gridx)
ax = krig.plot()
ax.scatter(cond_pos, cond_val, color="k", zorder=10, label="Conditions")
ax.legend()
Total running time of the script: ( 0 minutes 0.166 seconds)