Note
Go to the end to download the full example code
Introductory example
Let us start with a short example of a self defined model (Of course, we
provide a lot of predefined models [See: gstools.covmodel],
but they all work the same way).
Therefore we reimplement the Gaussian covariance model
by defining just the “normalized”
correlation
function:
import numpy as np
import gstools as gs
# use CovModel as the base-class
class Gau(gs.CovModel):
def cor(self, h):
return np.exp(-(h**2))
Here the parameter h stands for the normalized range r / len_scale.
Now we can instantiate this model:
model = Gau(dim=2, var=2.0, len_scale=10)
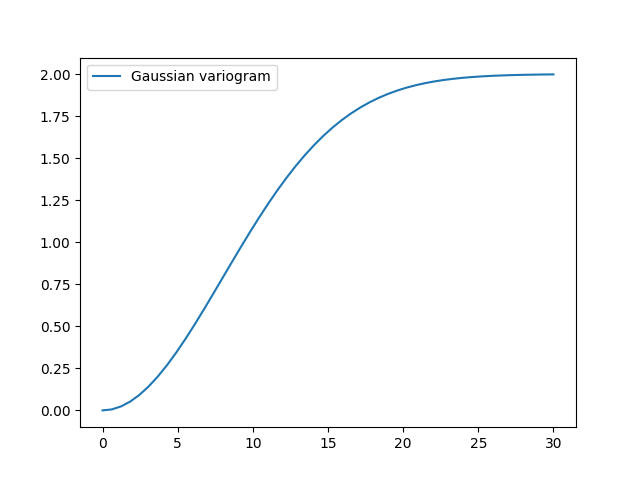
To have a look at the variogram, let’s plot it:
model.plot()

This is almost identical to the already provided Gaussian model.
There, a scaling factor is implemented so the len_scale coincides with the
integral scale:
gau_model = gs.Gaussian(dim=2, var=2.0, len_scale=10)
gau_model.plot()
Parameters
We already used some parameters, which every covariance models has. The basic ones are:
dim : dimension of the model
var : variance of the model (on top of the subscale variance)
len_scale : length scale of the model
nugget : nugget (subscale variance) of the model
These are the common parameters used to characterize a covariance model and are therefore used by every model in GSTools. You can also access and reset them:
print("old model:", model)
model.dim = 3
model.var = 1
model.len_scale = 15
model.nugget = 0.1
print("new model:", model)
old model: Gau(dim=2, var=2.0, len_scale=10.0, nugget=0.0)
new model: Gau(dim=3, var=1.0, len_scale=15.0, nugget=0.1)
Note
The sill of the variogram is calculated by
sill = variance + nuggetSo we treat the variance as everything above the nugget, which is sometimes called partial sill.A covariance model can also have additional parameters.
Total running time of the script: ( 0 minutes 0.295 seconds)