Creating Fancier Fields

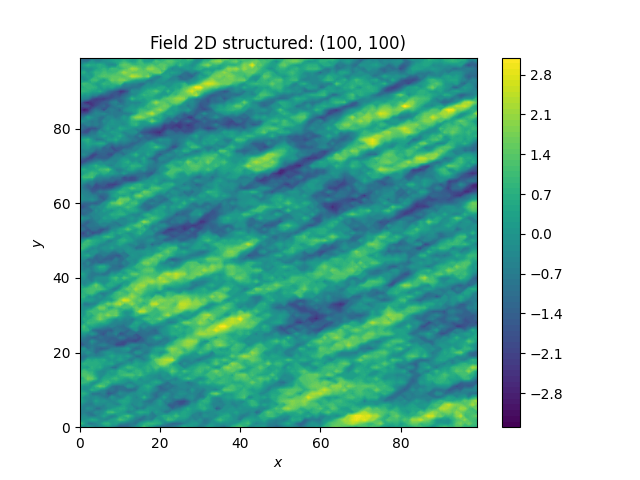
Only using Gaussian covariance fields gets boring. Now we are going to create much rougher random fields by using an exponential covariance model and we are going to make them anisotropic.

The code is very similar to the previous examples, but with a different covariance model class Exponential. As model parameters we a using following

• variance \(\sigma^2=1\)

• correlation length \(\lambda=(12, 3)^T\)

• rotation angle \(\theta=\pi/8\)

import numpy as np

import gstools as gs

x = y = np.arange(100)
model = gs.Exponential(dim=2, var=1, len_scale=[12.0, 3.0], angles=np.pi / 8)
srf = gs.SRF(model, seed=20170519)
srf.structured([x, y])
srf.plot()

The anisotropy ratio could also have been set with

model = gs.Exponential(dim=2, var=1, len_scale=12, anis=0.25, angles=np.pi / 8)