Note
Go to the end to download the full example code
Working with lat-lon random fields
In this example, we demonstrate how to generate a random field on geographical coordinates.
First we setup a model, with latlon=True, to get the associated
Yadrenko model.
In addition, we will use a kilometer scale provided by KM_SCALE
as geo_scale to have a meaningful length scale in km.
By default the length scale would be given in radians (RADIAN_SCALE).
A third option is a length scale in degrees (DEGREE_SCALE).
To generate the field, we simply pass (lat, lon) as the position tuple
to the SRF class.
import numpy as np
import gstools as gs
model = gs.Gaussian(latlon=True, len_scale=777, geo_scale=gs.KM_SCALE)
lat = lon = range(-80, 81)
srf = gs.SRF(model, seed=1234)
field = srf.structured((lat, lon))
srf.plot()
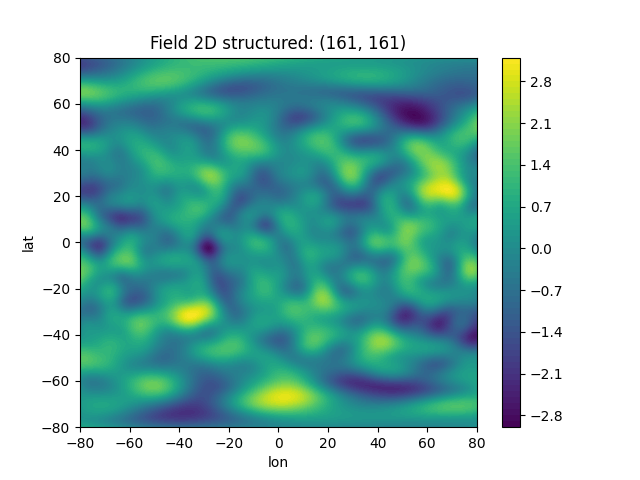
This was easy as always! Now we can use this field to estimate the empirical
variogram in order to prove, that the generated field has the correct
geo-statistical properties.
The vario_estimate routine also provides a latlon switch to
indicate, that the given field is defined on geographical variables.
As we will see, everthing went well… phew!
bin_edges = np.linspace(0, 777 * 3, 30)
bin_center, emp_vario = gs.vario_estimate(
(lat, lon),
field,
bin_edges,
latlon=True,
mesh_type="structured",
sampling_size=2000,
sampling_seed=12345,
geo_scale=gs.KM_SCALE,
)
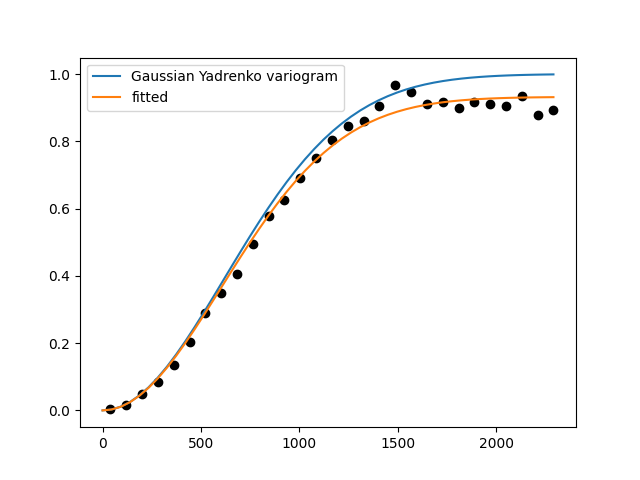
ax = model.plot("vario_yadrenko", x_max=max(bin_center))
model.fit_variogram(bin_center, emp_vario, nugget=False)
model.plot("vario_yadrenko", ax=ax, label="fitted", x_max=max(bin_center))
ax.scatter(bin_center, emp_vario, color="k")
print(model)
Gaussian(latlon=True, var=0.932, len_scale=7.57e+02, nugget=0.0, geo_scale=6.37e+03)
Note
Note, that the estimated variogram coincides with the yadrenko variogram, which means it depends on the great-circle distance given in radians.
Keep that in mind when defining bins: The range is at most \(\pi\approx 3.14\), which corresponds to the half globe.
Total running time of the script: ( 0 minutes 10.214 seconds)