Normalizing Data
When dealing with real-world data, one can’t assume it to be normal distributed. In fact, many properties are modeled by applying different transformations, for example conductivity is often assumed to be log-normal or precipitation is transformed using the famous box-cox power transformation.
These “normalizers” are often represented as parameteric power transforms and one is interested in finding the best parameter to gain normality in the input data.
This is of special interest when kriging should be applied, since the target variable of the kriging interpolation is assumed to be normal distributed.
GSTools provides a set of Normalizers and routines to automatically fit these to input data by minimizing the likelihood function.
Mean, Trend and Normalizers
All Field classes (SRF, Krige or CondSRF) provide the input
of mean, normalizer and trend:
A trend can be a callable function, that represents a trend in input data. For example a linear decrease of temperature with height.
The normalizer will be applied after the data was detrended, i.e. the trend was substracted from the data, in order to gain normality.
The mean is now interpreted as the mean of the normalized data. The user could also provide a callable mean, but it is mostly meant to be constant.
When no normalizer is given, trend and mean basically behave the same. We just decided that a trend is associated with raw data and a mean is used in the context of normally distributed data.
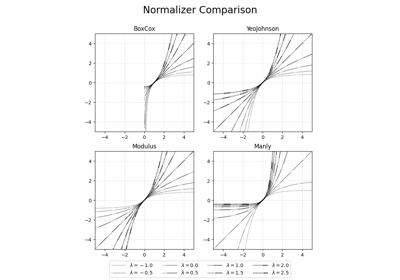
Provided Normalizers
The following normalizers can be passed to all Field-classes and variogram estimation routines or can be used as standalone tools to analyse data.
|
Log-normal fields. |
|
Box-Cox (1964) transformed fields. |
|
Box-Cox (1964) transformed fields including shifting. |
|
Yeo-Johnson (2000) transformed fields. |
|
Modulus or John-Draper (1980) transformed fields. |
|
Manly (1971) transformed fields. |