Note
Go to the end to download the full example code
Anisotropy and Rotation
The internally used (semi-) variogram represents the isotropic case for the model. Nevertheless, you can provide anisotropy ratios by:
import gstools as gs
model = gs.Gaussian(dim=3, var=2.0, len_scale=10, anis=0.5)
print(model.anis)
print(model.len_scale_vec)
[1. 0.5]
[10. 10. 5.]
As you can see, we defined just one anisotropy-ratio
and the second transversal direction was filled up with 1..
You can get the length-scales in each direction by
the attribute CovModel.len_scale_vec. For full control you can set
a list of anistropy ratios: anis=[0.5, 0.4].
Alternatively you can provide a list of length-scales:
model = gs.Gaussian(dim=3, var=2.0, len_scale=[10, 5, 4])
model.plot("vario_spatial")
print("Anisotropy representations:")
print("Anis. ratios:", model.anis)
print("Main length scale", model.len_scale)
print("All length scales", model.len_scale_vec)
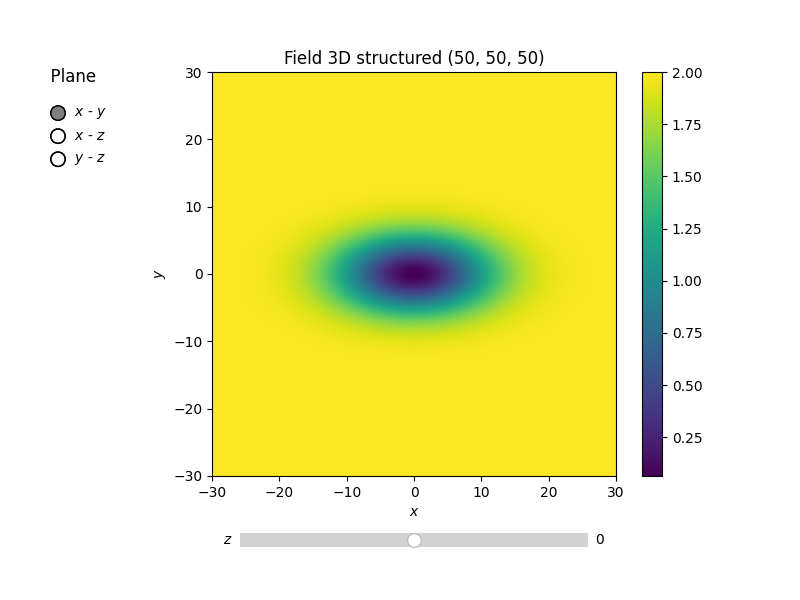
Anisotropy representations:
Anis. ratios: [0.5 0.4]
Main length scale 10.0
All length scales [10. 5. 4.]
Rotation Angles
The main directions of the field don’t have to coincide with the spatial directions \(x\), \(y\) and \(z\). Therefore you can provide rotation angles for the model:
model = gs.Gaussian(dim=3, var=2.0, len_scale=[10, 2], angles=2.5)
model.plot("vario_spatial")
print("Rotation angles", model.angles)
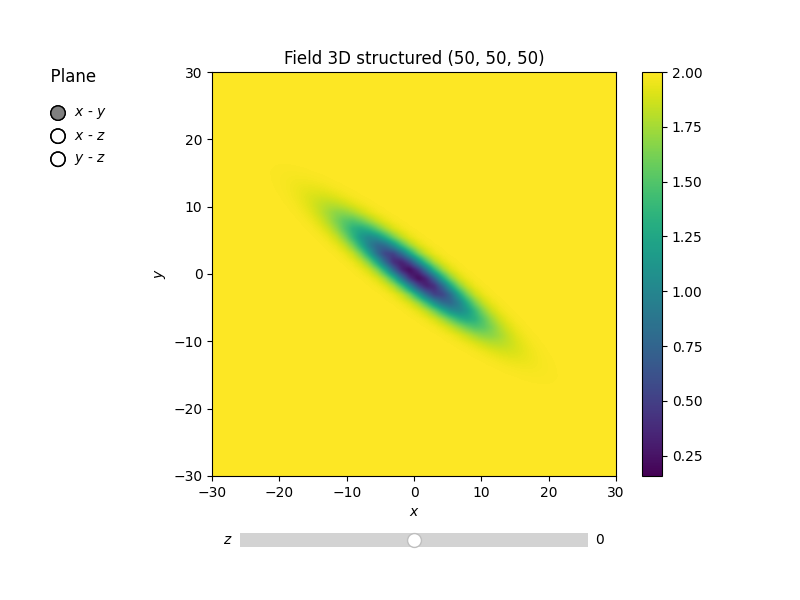
Rotation angles [2.5 0. 0. ]
Again, the angles were filled up with 0. to match the dimension and you
could also provide a list of angles. The number of angles depends on the
given dimension:
in 1D: no rotation performable
in 2D: given as rotation around z-axis
in 3D: given by yaw, pitch, and roll (known as Tait–Bryan angles)
in nD: See the random field example about higher dimensions
Total running time of the script: ( 0 minutes 1.023 seconds)