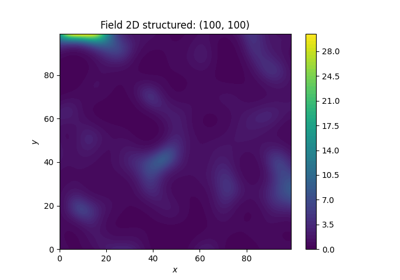
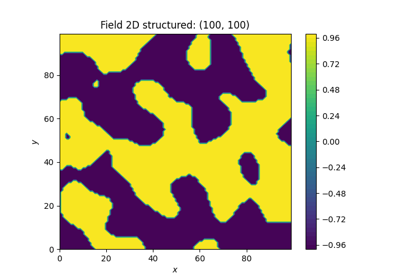
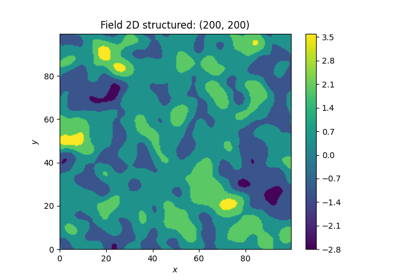
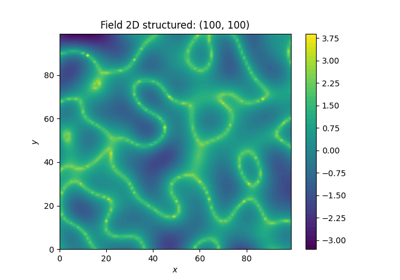
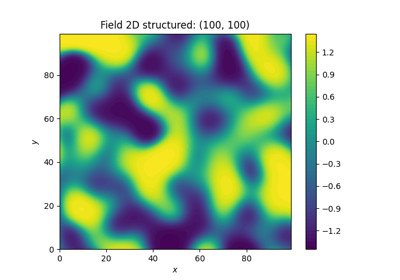
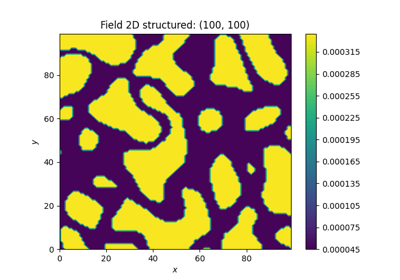
Field transformations
The generated fields of gstools are ordinary Gaussian random fields. In application there are several transformations to describe real world problems in an appropriate manner.
GStools provides a submodule gstools.transform with a range of
common transformations:
|
Binary transformation. |
|
Discrete transformation. |
|
(Inverse) Box-Cox transformation to denormalize data. |
|
Zinn and Harvey transformation to connect low or high values. |
|
Force moments of a normal distributed field. |
|
Transform normal distribution to log-normal distribution. |
|
Transform normal distribution to uniform distribution on [0, 1]. |
|
Transform normal distribution to the bimodal arcsin distribution. |
|
Transform normal distribution to U-quadratic distribution. |
|
Apply function as field transformation. |
All the transformations take a field class, that holds a generated field, as input and will manipulate this field inplace or store it with a given name.
Simply apply a transformation to a field class:
import gstools as gs
...
srf = gs.SRF(model)
srf(...)
gs.transform.normal_to_lognormal(srf)
Or use the provided wrapper:
import gstools as gs
...
srf = gs.SRF(model)
srf(...)
srf.transform("lognormal")