Note
Go to the end to download the full example code
Conditioning with Ordinary Kriging
Here we use ordinary kriging in 1D (for plotting reasons) with 5 given observations/conditions, to generate an ensemble of conditioned random fields.
import matplotlib.pyplot as plt
import numpy as np
import gstools as gs
# condtions
cond_pos = [0.3, 1.9, 1.1, 3.3, 4.7]
cond_val = [0.47, 0.56, 0.74, 1.47, 1.74]
gridx = np.linspace(0.0, 15.0, 151)
The conditioned spatial random field class depends on a Krige class in order to handle the conditions. This is created as described in the kriging tutorial.
Here we use a Gaussian covariance model and ordinary kriging for conditioning the spatial random field.
model = gs.Gaussian(dim=1, var=0.5, len_scale=1.5)
krige = gs.krige.Ordinary(model, cond_pos, cond_val)
cond_srf = gs.CondSRF(krige)
cond_srf.set_pos(gridx)
To generate the ensemble we will use a seed-generator. We can specify individual names for each field by the keyword store:
seed = gs.random.MasterRNG(20170519)
for i in range(100):
cond_srf(seed=seed(), store=f"f{i}")
label = "Conditioned ensemble" if i == 0 else None
plt.plot(gridx, cond_srf[f"f{i}"], color="k", alpha=0.1, label=label)
fields = [cond_srf[f"f{i}"] for i in range(100)]
plt.plot(gridx, cond_srf.krige(only_mean=True), label="estimated mean")
plt.plot(gridx, np.mean(fields, axis=0), linestyle=":", label="Ensemble mean")
plt.plot(gridx, cond_srf.krige.field, linestyle="dashed", label="kriged field")
plt.scatter(cond_pos, cond_val, color="k", zorder=10, label="Conditions")
# 99 percent confidence interval
conf = gs.tools.confidence_scaling(0.99)
plt.fill_between(
gridx,
cond_srf.krige.field - conf * np.sqrt(cond_srf.krige.krige_var),
cond_srf.krige.field + conf * np.sqrt(cond_srf.krige.krige_var),
alpha=0.3,
label="99% confidence interval",
)
plt.legend()
plt.show()
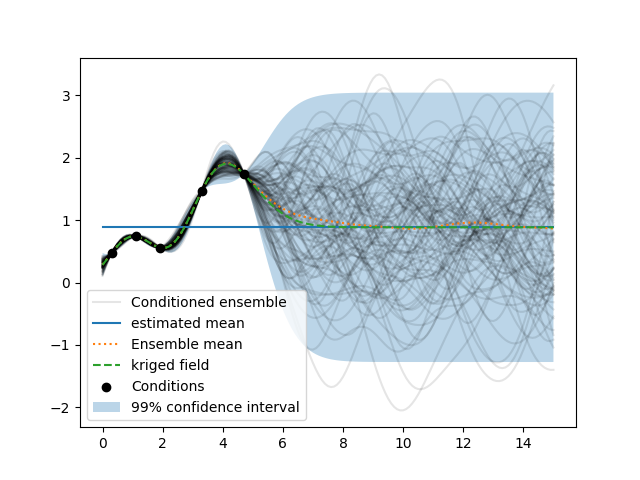
As you can see, the kriging field coincides with the ensemble mean of the conditioned random fields and the estimated mean is the mean of the far-field.
Total running time of the script: ( 0 minutes 1.353 seconds)