Note
Go to the end to download the full example code
Simple Kriging
Simple kriging assumes a known mean of the data. For simplicity we assume a mean of 0, which can be achieved by subtracting the mean from the observed values and subsequently adding it to the resulting data.
The resulting equation system for \(W\) is given by:
\[\begin{split}W = \begin{pmatrix}c(x_1,x_1) & \cdots & c(x_1,x_n) \\
\vdots & \ddots & \vdots \\
c(x_n,x_1) & \cdots & c(x_n,x_n)
\end{pmatrix}^{-1}
\begin{pmatrix}c(x_1,x_0) \\ \vdots \\ c(x_n,x_0) \end{pmatrix}\end{split}\]
Thereby \(c(x_i,x_j)\) is the covariance of the given observations.
Example
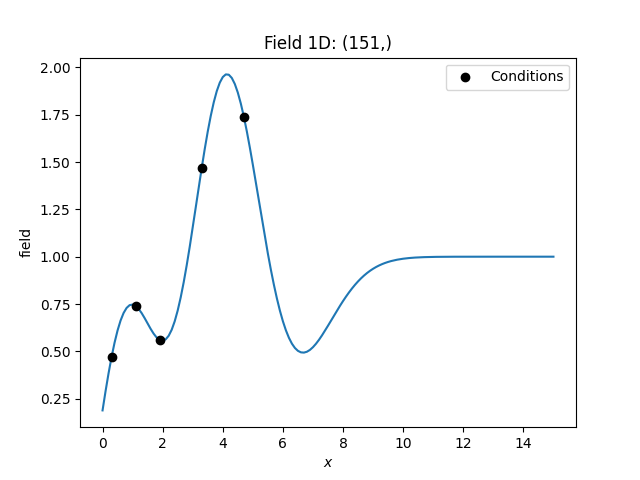
Here we use simple kriging in 1D (for plotting reasons) with 5 given observations/conditions. The mean of the field has to be given beforehand.
import numpy as np
from gstools import Gaussian, krige
# condtions
cond_pos = [0.3, 1.9, 1.1, 3.3, 4.7]
cond_val = [0.47, 0.56, 0.74, 1.47, 1.74]
# resulting grid
gridx = np.linspace(0.0, 15.0, 151)
# spatial random field class
model = Gaussian(dim=1, var=0.5, len_scale=2)
krig = krige.Simple(model, mean=1, cond_pos=cond_pos, cond_val=cond_val)
krig(gridx)
ax = krig.plot()
ax.scatter(cond_pos, cond_val, color="k", zorder=10, label="Conditions")
ax.legend()
Total running time of the script: ( 0 minutes 0.171 seconds)