Kriging
The subpackage gstools.krige provides routines for Gaussian process regression,
also known as kriging.
Kriging is a method of data interpolation based on predefined covariance models.
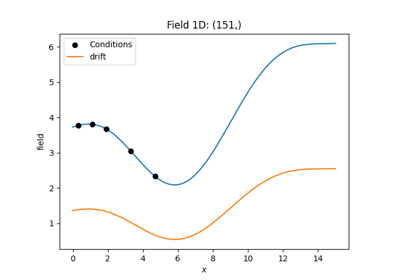
The aim of kriging is to derive the value of a field at some point \(x_0\), when there are fixed observed values \(z(x_1)\ldots z(x_n)\) at given points \(x_i\).
The resluting value \(z_0\) at \(x_0\) is calculated as a weighted mean:
The weights \(W = (w_1,\ldots,w_n)\) depent on the given covariance model and the location of the target point.
The different kriging approaches provide different ways of calculating \(W\).
The Krige class provides everything in one place and you can switch on/off
the features you want:
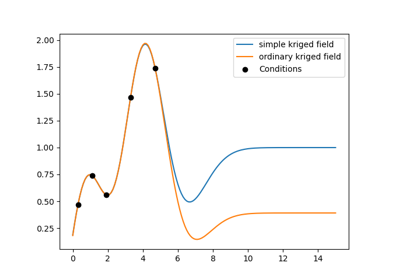
unbiased: the weights have to sum up to 1. If true, this results in
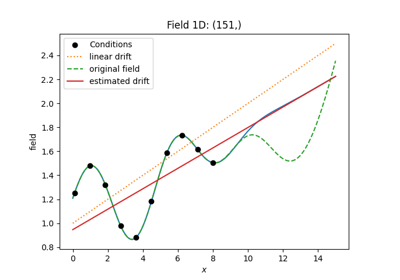
Ordinarykriging, where the mean is estimated, otherwise it will result inSimplekriging, where the mean has to be given.drift_functions: you can give a polynomial order or a list of self defined functions representing the internal drift of the given values. This drift will be fitted internally during the kriging interpolation. This results in
Universalkriging.ext_drift: You can also give an external drift per point to the routine. In contrast to the internal drift, that is evaluated at the desired points with the given functions, the external drift has to given for each point form an “external” source. This results in
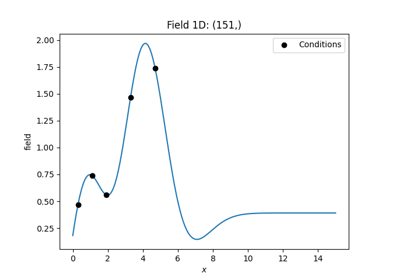
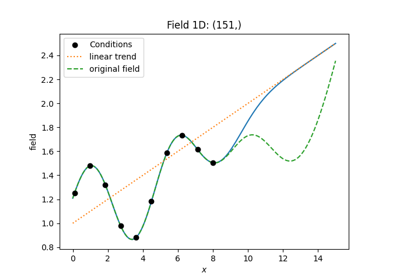
ExtDriftkriging.trend, mean, normalizer: These are used to pre- and post-process data. If you already have fitted a trend model that is provided as a callable function, you can give it to the kriging routine. Normalizer are power-transformations to gain normality. mean behaves similar to trend but is applied at another position:
conditioning data is de-trended (substracting trend)
detrended conditioning data is then normalized (in order to follow a normal distribution)
normalized conditioning data is set to zero mean (subtracting mean)
Cosequently, when there is no normalizer given, trend and mean are the same thing and only one should be used.
Detrendedkriging is a shortcut to provide only a trend and simple kriging with normal data.exact and cond_err: To incorporate the nugget effect and/or measurement errors, one can set exact to False and provide either individual measurement errors for each point or set the nugget as a constant measurement error everywhere.
pseudo_inv: Sometimes the inversion of the kriging matrix can be numerically unstable. This occurs for examples in cases of redundant input values. In this case we provide a switch to use the pseudo-inverse of the matrix. Then redundant conditional values will automatically be averaged.
Note
All mentioned features can be combined within the Krige class.
All other kriging classes are just shortcuts to this class with a limited list
of input parameters.
The routines for kriging are almost identical to the routines for spatial random fields, with regard to their handling. First you define a covariance model, as described in The Covariance Model, then you initialize the kriging class with this model:
import gstools as gs
# condtions
cond_pos = [...]
cond_val = [...]
model = gs.Gaussian(dim=1, var=0.5, len_scale=2)
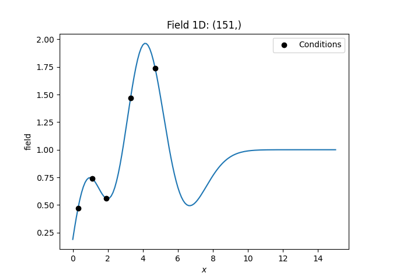
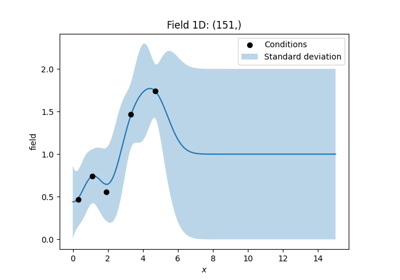
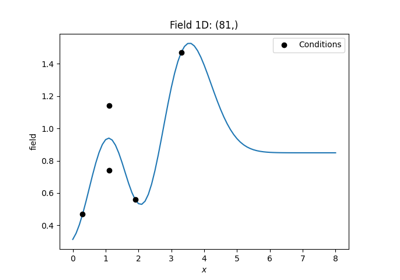
krig = gs.krige.Simple(model, cond_pos=cond_pos, cond_val=cond_val, mean=1)
The resulting field instance krig has the same methods as the
SRF class.
You can call it to evaluate the kriged field at different points,
you can plot the latest field or you can export the field and so on.
Provided Kriging Methods
The following kriging methods are provided within the
submodule gstools.krige.
|
A Swiss Army knife for kriging. |
|
Simple kriging. |
|
Ordinary kriging. |
|
Universal kriging. |
|
External drift kriging (EDK). |
|
Detrended simple kriging. |